Properties of Cross Product Physics Notes
Properties of cross product:
1. Vector products do not show commutative property:
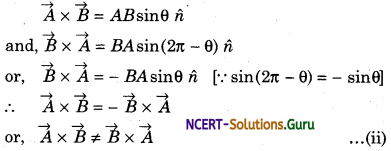
2. Vector Product of Two Parallel Vectors:
Let \(\vec{A}\) and \(\vec{B}\) be two parallel vector. So, the angle between the two vectors, θ = 0°.
From vector products,
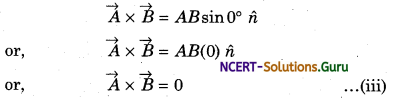
So, the vector product of two parallel vectors is a zero product.
![]()
3. Vector Product of Equal Vectors: Equal vectors are also parallel. So, the angle between them will also be zero. So, θ = 0°.
∴ \(\vec{A} \times \vec{A}\) = AA sin 0° = 0
So, the vector product of equal vectors is a zero vector.
∴ î × î = ĵ × ĵ = k̂ × k̂ = 0 …(iv)
4. Vector Product of Perpendicular:
Vectors: Let us assume that \(\vec{A}\) and \(\vec{B}\) are two vectors perpendicular to each other. So, the angle between them will be 90°, i.e., θ = 90°.
Then,
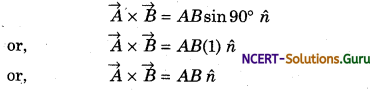
Here, the direction of ñ is according to the right-hand rule, in the direction perpendicular to the plane of \(\vec{A}\) and \(\vec{B}\). So, in this way,
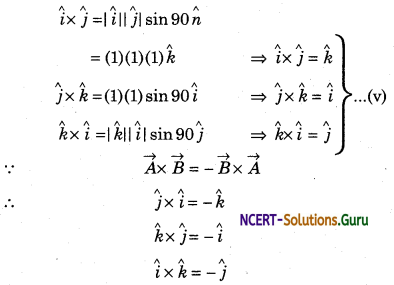
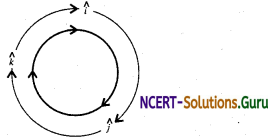
If î, ĵ, and k̂ are in the cyclic order (clockwise) then the vector product is positive and if not in cyclic then the product will be negative.
![]()
5. Vector Product in the form of a Determinant: If the vectors are expressed in terms of unit vectors î, ĵ and k̂ in the X, Y, and Z directions, then the vectors can be expressed as:

Using equations (iv) and (v), we have
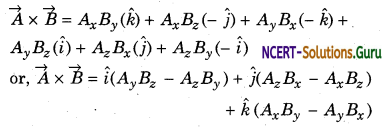
It can be re-written in the form of determinants
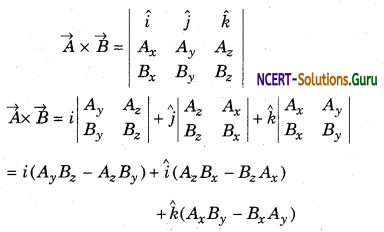
The magnitude of cross product:

![]()
6. Cross product of two vectors is distributive:
i. e., \(\vec{A} \times(\vec{B}+\vec{C})=\vec{A} \times \vec{B}+\vec{B} \times \vec{C}\)
7. Cross product of two vectors is associative i.e.,
\((\vec{A}+\vec{B}) \times(\vec{C}+\vec{D})=\vec{A} \times \vec{C}+\vec{A} \times \vec{D}+\vec{B} \times \vec{C}+\vec{B} \times \vec{D}\)
8. Examples of Some Physical Quantities Obtained from Vector Product
(a) Let \(\vec{L}\) and \(\vec{B}\) respectively be the adjacent sides of a parallelogram, then the area of it will be:
\(\vec{A}=\vec{L} \times \vec{B}\)
(b) Torque (\(\vec{τ}\)), displacement (\(\vec{r}\)) and force (\(\vec{F}\)) are associated as:
\(\vec{\tau}=\vec{r} \times \vec{F}\)
i.e., torque (\(\vec{τ}\)) is the cross product of displacement and force.
(c) Angular momentum (J), displacement (\(\vec{r}\)) and linear momentum (\(\vec{p}\)) are associated as:
\(\vec{J}=\vec{r} \times \vec{p}\)
i. e., angular momentum is equal to the cross-product of displacement and linear momentum.
![]()
(d) Angular velocity (ω), linear velocity (v) and displacement (r) are associated as :
\(\vec{v}=\vec{\omega} \times \vec{r}\)
i.e., linear velocity is equal\o the cross-product of angular velocity and displacemerí.
(e) The vectors of adjacent sidef a triangle are and b the area of triangle:
\(\vec{A}=\frac{1}{2}|\vec{a} \times \vec{b}|\)